[コンプリート!] a^3 b^3 c^3=(a b c)^3 157001-A^3+b^3+c^3=3abc a+b+c=
A^3 b^3 c^3 = d^3 Reading about Fermat's Last Theorem again, and once again I find myself wondering about positive integer solutions of a 3 b 3 c 3 = d 3 Over the years, I have never been able to find any information about such a trivial problem, but I must not know how to ask the question properly or where to lookProve that (a b c)^3 a^3 b^3 c^3 = 3 (a b ) (b c) (c a)Share It On Facebook Twitter Email 1 Answer 1 vote answered Nov 10, 18 by Sanaa (118k points) selected Nov 10
View Question If A B 8 B C 3 And A C 5 What Is The Value Of The Product Abc
A^3+b^3+c^3=3abc a+b+c=
A^3+b^3+c^3=3abc a+b+c=-Sides a = 3 b = 4 c = 5 Area T = 6 Perimeter p = 12 Semiperimeter s = 6 Angle ∠ · Then take c=a and also sheres on ca(abc)^3a^3b^3c^3 =k(ab)(bc)(ca) K is unknown, so find her If a=1,b=1,c=0》(110)^31^31^30=k (11)(10)(01) =k*2 K=3 (abc)^3a^3b^3c^3 =3 (ab)(bc)(ca) October 29, 15 at 841 PM




Inequalities Marathon
· Best Answer Thanks guest, that is a great answer I just wanted to think about it a little There are an infinite number of answers (a)^3 (b)^3 (c)^3 = 33B ≤ ≤ 0 chứng minh a 3 b 3 ≤ ≤ ab* (ab) Theo dõi Vi phạm YOMEDIAFactor (a^2b^2)^3(b^2c^2)^3(c^2a^2)^3 Use the Binomial Theorem Simplify each term Tap for more steps Multiply the exponents in Tap for more steps Apply the power rule and multiply exponents, Multiply by Rewrite using the commutative property of multiplication Multiply by
A 3 b 3 = (a b) (a² – ab b² ) Somme de deux cubes divisible par somme des nombres Ex 9 3 9 3 = 18 x 81 a 3 c 3 Quelle que soit la valeur de b = = (a – b) (a² ab b² ) (c b) (c² – cb b² ) (a 3 – b 3) (c 3 b 3 ) a 3 b 3 c 3 – 3abc = (a b c) (a² b² c² – · let therefore and using the identity therefore hope this helps you cheers!!As stated in the title, I'm supposed to show that ( a b c) 3 = a 3 b 3 c 3 ( a b c) ( a b a c b c) My reasoning ( a b c) 3 = ( a b) c 3 = ( a b) 3 3 ( a b) 2 c 3 ( a b) c 2 c 3 ( a b c) 3 = ( a 3 3 a 2 b 3 a b 2 b 3) 3 ( a 2 2 a b b 2) c 3 ( a b) c 2 c 3
7/08/17 · Explanation Considering that (a b c)3 − (a3 b3 c3 −3abc) = 3(a b c)(ab bc ac) then if (a b c) ≠ 0 we have (a b c)2 = 3(ab bc ac) and finally a b c = ± √3√ab bc ac NOTE 0 = (a b c)2 − 3(ab bc ac) = a2 b2 c2 −(ab ac bc) = 1 2 ((a − b)2 (b − c)2 (a −c)2) = 0 Answer linkCác hằng đẳng thức Bình phương của một tổng ( a b ) 2 = a 2 2 a b b 2 {\displaystyle (ab)^ {2}=a^ {2}2abb^ {2}\,} Bình phương của một hiệu ( a − b ) 2 = a 2 − 2 a b b 2 {\displaystyle (ab)^ {2}=a^ {2}2abb^ {2}\,} Hiệu hai bình phương6/03/19 · There are various student are search formula of (ab)^3 and a^3b^3 Now I am going to explain everything below You can check and revert back if you like you can also check cube formula in algebra formula sheet a 2 – b 2 = (a – b) (a b) (ab) 2 = a 2 2ab b 2 a 2 b 2 = (a – b




Important Question With Trick Powerpoint Slides




ユニークab Ca 子供のための最高のぬりえ
· (abc)3 New Resources Kopia Surface Area for Cuboid;Equations Tiger Algebra gives you not only the answers, but also the complete step by step method for solving your equations a(bc)^3b(ca)^3c(ab)^3 so that you understand better · Using properties of determinants, prove the following (bc,ab,a)(ca,bc,b)(a=b,ca,c) = 3abca^3b^3c^3 asked Nov 10, 18 in Mathematics by Aria ( 60k points) determinant



Search Q A 5e3 2bb 5e3 2bc 5e3 3abc Formula Tbm Isch




In A Certain Country 1 2 Of 5 3 If The Sam Math Puzzles Questions Answers Sawaal
(abc) 3 a 3 b 3 c 3 We can choose three "a"'s for the cube in one way C(3,3)=1, or we can choose an a from the first factor and one from the second and one from the third, being the only way to make a3 The coefficient of the cubes is therefore 1 (It's the same for a, b and c, of course) 3a 2 b3a 2 c Next, we consider the a 2 termsGet the answer to this question by visiting BYJU'S Q&A ForumWatch Blue Bayou (21) Full Online Movie free HD
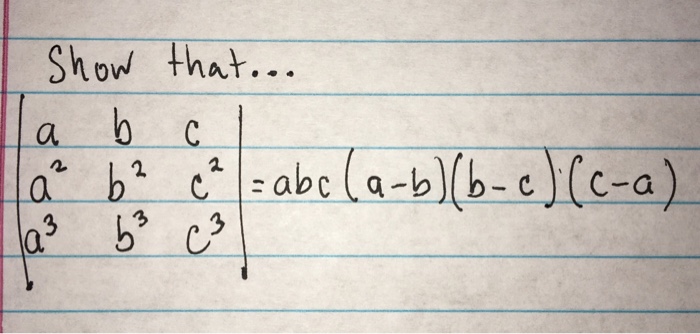



Matrix A B C A 2 B 2 C 2 A 3 B 3 C 3 Chegg Com




Prove The A B C 3 A 3 B 3 C 3 3 A B B C C A Brainly In
Chứng minh tương tự ta có b^3b chia hết cho 3 và c^3c chia hết cho 3 với mọi b,c thuộc Z => a 3 b 3 c 3 (abc) luôn chia hết cho 3 với mọi a,b,c thuộc Z => nếu a 3 b 3 c 3 chia hết cho 3 thì abc chia hết cho 3 và điều ngược lại cũng đúng Vậy đpcmchúc bn hok tốt8/10/ · a 3 b 3 = (a b) (a 2 b 2 − ab) (a b c) 3 = a 3 b 3 c 3 3 (a b) (b c) (c a) a 3 b 3 c 3 − 3abc = (a b c) (a 2 b 2 c 2 − ab − bc − ac) If (a b c) = 0, a 3 b 3 c 3/03/08 · So basically what it is is that the problem is a^3b^3=c^3 but you changed it to cube root a^3 cube rootb^3 =cube rootc^3 which is equal to ab=c, so if what you say is right you would be able to use any terms for this second equation and it would fit the third




Show That Det 1 1 1 1 A B C D A 2 B 2 C 2 D 2 Chegg Com




Math Triangle Abc Math With Vertices A 1 2 B 3 1 And C 3 4 Translated 2 Units Left And 1 Unit Up Homework Help And Answers Slader
3 x n3 a3 nC n a n nth term, T r1 = nCr x nr ar PARTIAL FRACTIONS f(x) g(x) is a proper fraction if the deg (g(x)) > deg (f(x)) f(x) g(x) is a improper fraction if the deg (g(x)) ≤ deg (f(x)) 1 Linear non repeated factors f(x) A B (ax b)(cx d) ax b (cx d) = 2 Linear repeated factors 2 2 f(x) A B C (ax b)(cx d) axTo simplify the above expressions, start by expanding the binomials Note that we can expand the (ab)^3 , (bc)^3 , and (ca)^3 using the special product formulas for a cube of a binomial · What is the formula for (a^3 b^3)?
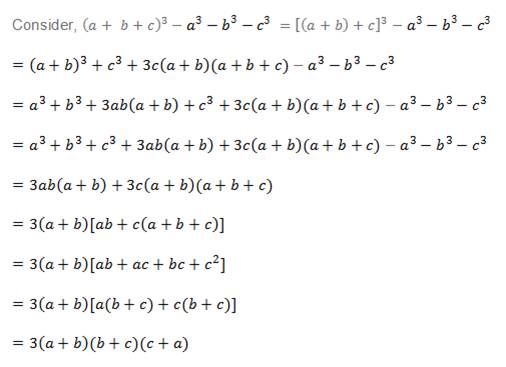



Prove That A B C 3 A3 C3 3 A B B C C A Home Work Help Learn Cbse Forum



If A B C 0 Then Find The Value Of B2 Ca C2 Ab Polynomials Maths Class 9
Solve for c A=(abc)/3 Rewrite the equation as Multiply both sides of the equation by Cancel the common factor of Tap for more steps Cancel the common factor Rewrite the expression Move all terms not containing to the right side of the equation Tap for more stepsTiger was unable to solve based on your input (ab)3(bc)3(ca)3 Step by step solution Step 1 11 Evaluate (ca)3 = c33ac23a2ca3 Step 2 Pulling out like terms 21 · cho a b c = 0Chứng minh a^3 b^3 c^3 =3abc Lỗi Trang web OLMVN không tải hết được tài nguyên,




Hardest Mathematics Problem Toughest Algebra Problem World S Toughest Maths Problem Q 2 Apho18




Using Properties Of Determinants Prove That A B C A B B C C A A 3 B 3 C 3 3abc B C C A A B Mathematics Topperlearning Com Dteg67ff
· a3 b3 c3 – 3abc = (a b c) (a2 b2 c2 – ab – ac – bc) a3 b3 c3=3abc 21, Haziran, 15 galois95 (15 puan) tarafından cevaplandı ilgili bir soru sor Lütfen yorum eklemek için giriş yapınız veya kayıt olunuzI suggests that you use (ab)^3=a^3b^33ab(ab)\Rightarrow a^3b^3=(ab)^33ab(ab) instead, you will need to use it twice like this a^3b^3c^33abc =(ab)^3c^33ab(ab)3abc =(abc)^3(3c(ab)^23(ab)c^2)3ab(abc) · Chứng minh rằng (a^3/a^2abb^2) (b^3/b^2bcc^2) (c^3/c^2aca^2)>=abc/3 Cho a,b, c là các số thực dương CMR a3 a2 ab b2 b3 b2 bc c2 c3 c2 ac a2 ≥ a b c 3 a 3 a 2 a b b 2 b 3 b 2 b c c 2 c 3 c 2 a c a 2 ≥ a b c 3 Theo dõi Vi phạm YOMEDIA Toán 9 Chương 3 Bài 7 Trắc




Algebra Toughest Questions Algebra Teaching Mathematics




In Triangle Abc If S 3 3 2 3b C 30 O A 2b 1 O Where A B C Are Respective Angles Then The
Since, a3 b3 c3 −3abc= (abc)(a2 b2 c2 −bc−ca−ab) Given, abc = 0 ∴ a3 b3 c3 −3abc = 0 ∴ a3 b3 c3 =3abc Option B is correct Answer verified by Toppr Upvote (0)7/06/18 · if x1/x=5,then find value of x^31/x^3 The valuesof 249square 248square is 729X3512y3 Factorise (abc)³a³b³c3 I need very urgently please answer as quickly as you can Experts, please help me with the following questions attached below in the image Questions are from chapter POLYNOMIALS, grade 9 (please answer all of themExample Solve 8a 3 27b 3 125c 3 – 90abc Solution This proceeds as Given polynomial (8a 3 27b 3 125c 3 – 90abc) can be written as (2a) 3 (3b) 3 (5c) 3 – 3(2a)(3b)(5c) And this represents identity a 3 b 3 c 3 3abc = (a b c)(a 2 b 2 c 2 ab bc ca) Where a = 2a, b = 3b and c = 5c Now apply values of a, b and c on the LHS of identity ie a 3 b 3 c 3
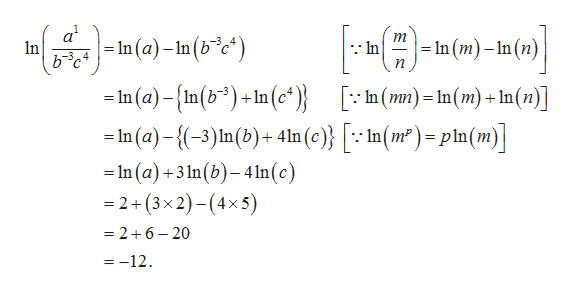



Answered If Ln A 2 Ln B 3 And Ln C 5 Bartleby




Art Of Problem Solving
· c=3 Nuevas preguntas de Matemáticas N Convierte las longitudes a las uñidades indicadas a 7000 km m b cm dam C 276 km cm d 17,6 cm mm DET 25 · a^3 b^3 c^3 a 3 b 3 c 3 = (a b c) (a 2 b 2 c 2 – ab – bc – ca) 3abc s Algebra, cube, sum, sum of cubes This entry was posted on June 21, 08 at 554 pm and is filed under Algebra You can follow any responses to this entry through the RSS feed You can leave a response, or trackback from your own siteChứng minh a^3b^3 < = ab (ab) biết a < = 0, b < = 0 cho a ≤ ≤ 0 ;




Could You Easily Decompose A 3 B 3 C 3 3abc Into The Product Of Two Polynomials With Real Coefficients




If A B C 6 And Ab Ca 11 Find The Value Of A 3 B 3 C 3 3abc Cbse Class 9 Maths Learn Cbse Forum
A 3 b 3 c 33abc=(ab) 33a 2 b3ab 2 c 33abc =(abc) 3 3(ab) 2 c3(ab)c 2 3ab(abc) =(abc) 3 3(ab)c(abc)3ab(abc)=(abc)(a 2 b 2 c 2 abbcac) · a^3b^3等于多少? #热议# 六一儿童节送什么礼物好?Simple and best practice solution for A=(4C) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so




A 3 B 3 C 3 Formula Brainly In



Prove That A B C 3 A3 C3 3 A B B C C A Studyrankersonline
两数差乘以它们的平方和与它们的积的和等于两数的立方差。 你对这个回答的评价是? ③立方和公式:a3b3= (ab) (a2abb2) 立方差公式:a3b3= (ab) (a2abb2) 你对这个回答的评价是?2/07/ · Proof Formula \((abc)^3 = \\a^3 b^3 c^3 6abc \\ 3ab (ab) 3ac (ac) 3bc (bc) \) Summary (abc)^3 If you have any issues in the (abc)^3 formulas, please let me know through social media and mail A Plus B Plus C Whole cube is most important algebra maths formulas for class 6 to 12A = α = 368 7 ° = 36°52'12″ = 064 4 rad Angle ∠



If Math A B C 1 Math Math A 2 B 2 C 2 2 Math And Math A 3 B 3 C 3 3 Math Then What Is Math A Times B Times C Math Quora



Solved Show That The Triangle With Vertices A 0 2 B 3 1 And C 4 3 Is Isosceles Triangle Abc Consists Of Points A 2 2 B 3 1 And C 3 3 Course Hero
· Suppose a^3 b^3 = c^3 with (a,b,c) = 1 Let (1) a b = c x Cubing, (2) a^3 3a^2(b) 3(a)b^2 c^3 = c^3 3c^2(x) 3(c)x^2 x^3 Subtracting a^3 b^3 = c^3, (3) 3ab(a b) = 3cx(c x) x^3 Transposing and substituting (1), (4) 3(a b)(ab cx) = x^3 · (abc)^3a^3b^3c^3 ={(ab)c}^3 a^3b^3c^3 =(ab)^3c^33c(ab)(abc)a^3b^3c^3 =a^3b^3c^33ab(ab)3c(ab)(abc)a^3b^3c^3=3ab(ab)3c(ab)(abc)=3(ab){abc(abc)}=3(ab){abacbcc^3}=3(ab){a(bc)c(bc)} =3(ab)(bc)(ca)B = β = 531 3 ° = 53°7'48″ = 092 7 rad Angle ∠




If A3 C3 3abc 1 2 A B C A B 2 B C 2 C A 2 Brainly In



Using Properties Of Determinants Show The Following B C 2 Ab Ca Ab A C 2 Ac A B 2 2abc A B C 3 Sarthaks Econnect Largest Online Education Community
· a^3b^3c^33abc = (ab) (a^2abb^2)c (c^23ab) = (ab) (a^2abb^2)c (c^23aba^2abb^2a^2abb^2) = (ab) (a^2abb^2)c (c^2a^22abb^2) (a^2abb^2) = (ab) (a^2abb^2)c c^2 (ab)^2c (a^2abb^2) = (abc) (a^2abb^2)c (abc) (cab) = (abc) (a^2b^2c^2abbcac) 好评,,谢谢啦 本回答被网友采纳 · Using properties of determinants, prove the following (bc,ab,a)(ca,bc,b)(a=b,ca,c) = 3abca 3b 3c 3 determinant;Since the formula for (abc)^3 is (abc) ^3 = a^3b^3 c^3 3ab3bc3ac Then by rearranging the formula we can get a^3b^3c^3 =(abc)^3–3ab 3bc3ac




Sat Ii Math Level 2 Test 05 Solution 1 If 8x 12 K 3 2x 3 For All X Then K A 1 4 B 3 C 4 D 12 E 24 8x 12 K 3 2x 3 Ppt Download




Lecture 34 Section 6 7 Wed Mar 28 Ppt Video Online Download
/11/12 · RE Beweis der Ungleichung a^3 b^3 c^3 >= 3abc Hallo Mystic, ich habe anstelle der drei Zahlen a,b,c die dritte Potenz dieser Zahlen verwendet, da sich hierdurch nicht das Vorzeichen umkehrt Ich bin davon ausgegangen, dass die Relation "arithmetisches Mittel" >= "geometrisches Mittel" weiterhin gültig bleibt 1112, 09298/07/17 · views around the world You can reuse this answer Creative Commons LicenseIdentités remarquables de degré 3 (a b) 3 = a 3 3a²b 3ab² b 3 (a b) 3 = a 3 3a²b 3ab² b 3 pour comprendre cette identité remarquable, on peut construire un cube de côté (a b) et exprimer de deux façons le volume du cube




Here Is A Proof That 3 4 Let A B And C Be Any Chegg Com




Misc 13 Using Determinants 3 A B C Ab Ac
3/01/21 · You can see that if you expand (abc)^2, simplify, multiply by 2, and use the trivial inequality Instead of doing AMGM, I managed to solve it using CauchySchwartz Inequality There is likely a solution with AMGM, but I don't see it So here is mine (a 3 b 3 c 3 ) (abbcca) ≥abc (abc) 2 Divide all by abcPhân tích thành nhân tử a a3 b3 c3 – 3abc b (x y)3 (y z)3 (z x)3 Loga Toán lớp 8 0 lượt thích 445 xem 1 trả lời Thích Trả lời Chia sẻ Crayed0603 a, \ (a^3b^3c^33abc\)C = γ = 90° = 157 1 rad Height h a = 4 Height h b = 3 Height h c = 24 Median m a




Prove A 3 B 3 C 3 3abc 1 2 A B C A B 2 B C 2 C A 2



Www Pmschools Org Site Handlers Filedownload Ashx Moduleinstanceid 701 Dataid 3614 Filename 15 composition of transformations answers Pdf




Inequalities Marathon




Multinomial Expansion




Michael Rozenberg S Inequality In Three Variables With Constraints




If A B C 6 A 2 B 2 C 2 14 A 3 B 3 C 3 36 Find Abc Youtube




What Are Various Forms To Write A B C A Whole Cube Quora




A3b3c3 3abc Formula Proof រ បភ ពប ល ក Images




Prove That A3 C3 3abc A B C X Where H Chegg Com



Http Services Aops Com Download Php Id Yxr0ywnobwvudhmvyi80lzg3mge4ywm2ntbkmtfjy2q4nmi4zwfinzu5mgvkmgm2nje2otjllnbkzg Rn Q2hhchrlciaynsbbts1htsbjbmvxdwfsaxrpzxmucgrm



1




A3b3c3 3abc Formula Proof រ បភ ពប ល ក Images




View Question If A B 8 B C 3 And A C 5 What Is The Value Of The Product Abc
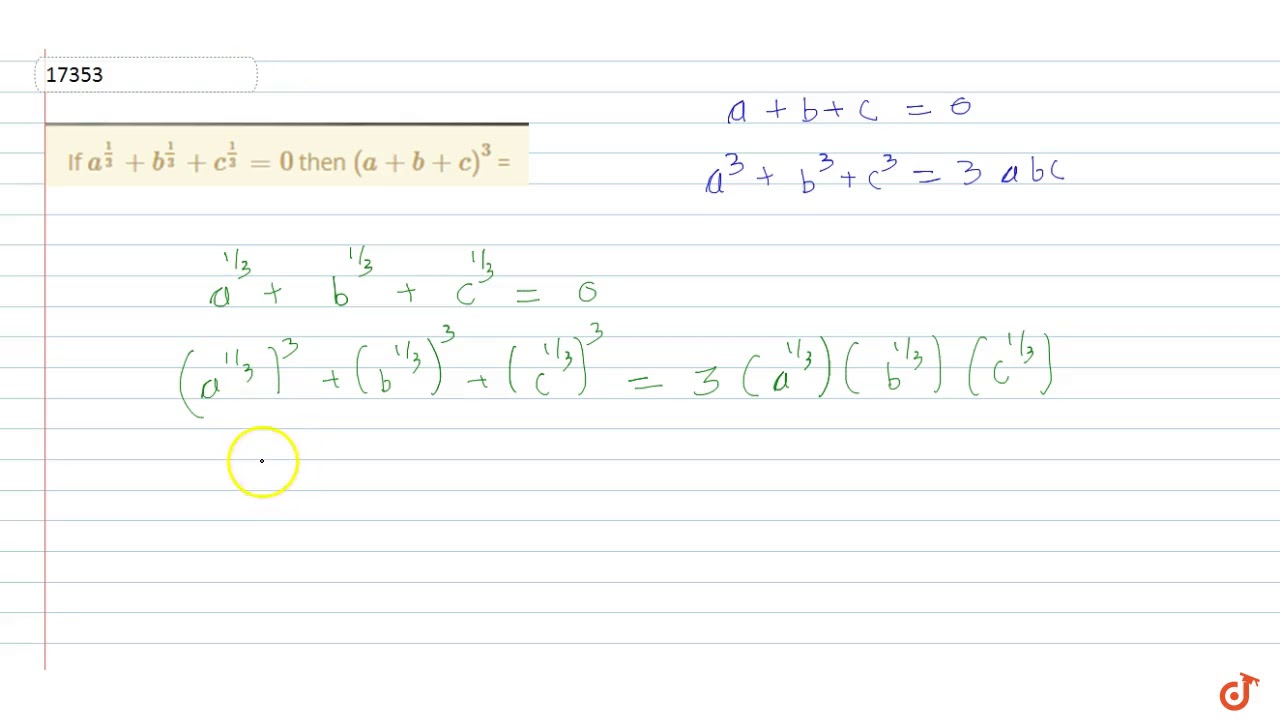



If A 1 3 B 1 3 C 1 3 0 Then A B C 3 Youtube




Question Prove That A B C 3 Ndash A3 C3 3 A B B C C A Mathematics Topperlearning Com We5wwhmm




What Is The Expansion Of A B C 3 Quora




If A B C 0 Then A 3 B 3 C 3 0 How Quora




Example 3 Let A 1 2 3 B 3 4 And C 4 5 6




If A B C 5 And Ab Ca 10 Prove A 3 B 3 C 3 3abc 25 Cbse Class 9 Maths Learn Cbse Forum



If A B C 0 Then How Can You Prove A 3 B 3 C 3 3abc Quora



If A B C 5 And Ab Ca 10 Then Prove That A3 C3 3abc 25 Studyrankersonline



A Factor Of A B C 3 A3 C3 With Solution Askiitians




Inequalities Marathon




Simplify A 2 B 2 3 B 2 C 2 3 C 2 A 2 3 A B 3 B C 3 C A 3




Prove That A 3 B 3 C 3 Abc 1 2 A B C A B 2 B C 2 C A 2 Maths Polynomials Meritnation Com



If Math A B C 1 Math Math A 2 B 2 C 2 2 Math And Math A 3 B 3 C 3 3 Math Then What Is Math A Times B Times C Math Quora




If A 1 3 B 1 3 C 1 3 0 Then A A B C 0 B A B C 3 27 A B C C A B C 3 Youtube



If A B C 0 Then How Can You Prove A 3 B 3 C 3 3abc Quora




Ab Cd Abcd Xcxd Abcabd Acbcadbd Abcd Acbcadbd
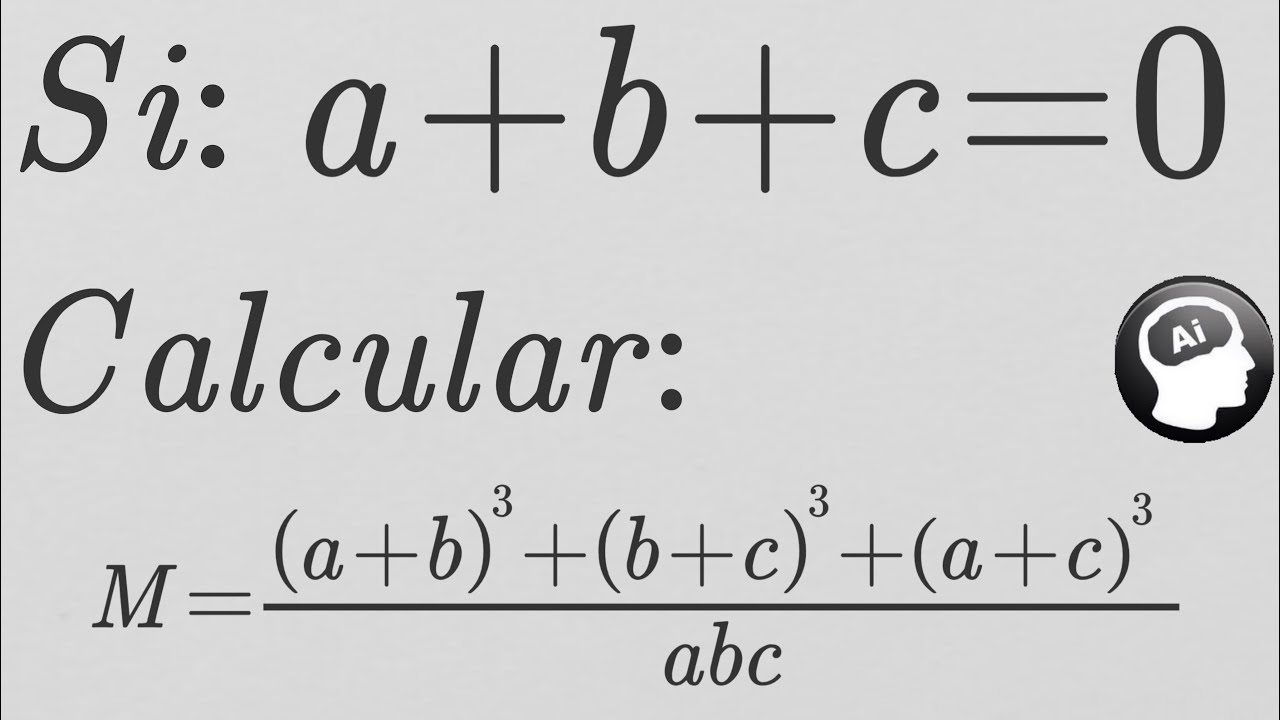



Si A B C 0 A 3 B 3 C 3 3abc Youtube




Prove A3 C3 3abc A B C B2 C2 Ab Ac Youtube




Prove That A B C 3 A 3 B 3 C 3 3 A B B C C A Youtube



Abc3 Formula Expansion រ បភ ពប ល ក Images



Using Properties Of Determinants Prove The Following A B C A B B C C A B C C A A B A3 C3 3abc Sarthaks Econnect Largest Online Education Community




1 Let A 1 2 3 4 And B A B C D Determine Which Chegg Com




If A B C 0 Then Find The Value Of A3 C3 Tex If A B C 0 Then Find The Value Of A 3 Brainly In




Inequalities Marathon




The Value Of A 3 B 3 C 3 3abc Ab Ca A 2 B 2 C 2 Is Where




If A B C 2 Ab Ca 1 And Abc 1 And Abc 2 Find The Value Of




Ab Cd Abcd Xcxd Abcabd Acbcadbd Abcd Acbcadbd



Q Tbn And9gcsn3hmt8qz Utmzoqeyjo2k4rnk95kuib8fxbhmd Uvs2llqap Usqp Cau




If A B 1 2 3 8 B C 1 3 5 9 A N D C D 5 6 3 4 Then The Ratio A B C D Is 4 6 8 Youtube
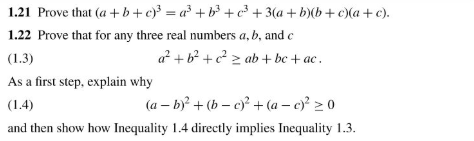



1 21 Prove That A B C 3 A3 C3 3 A Chegg Com
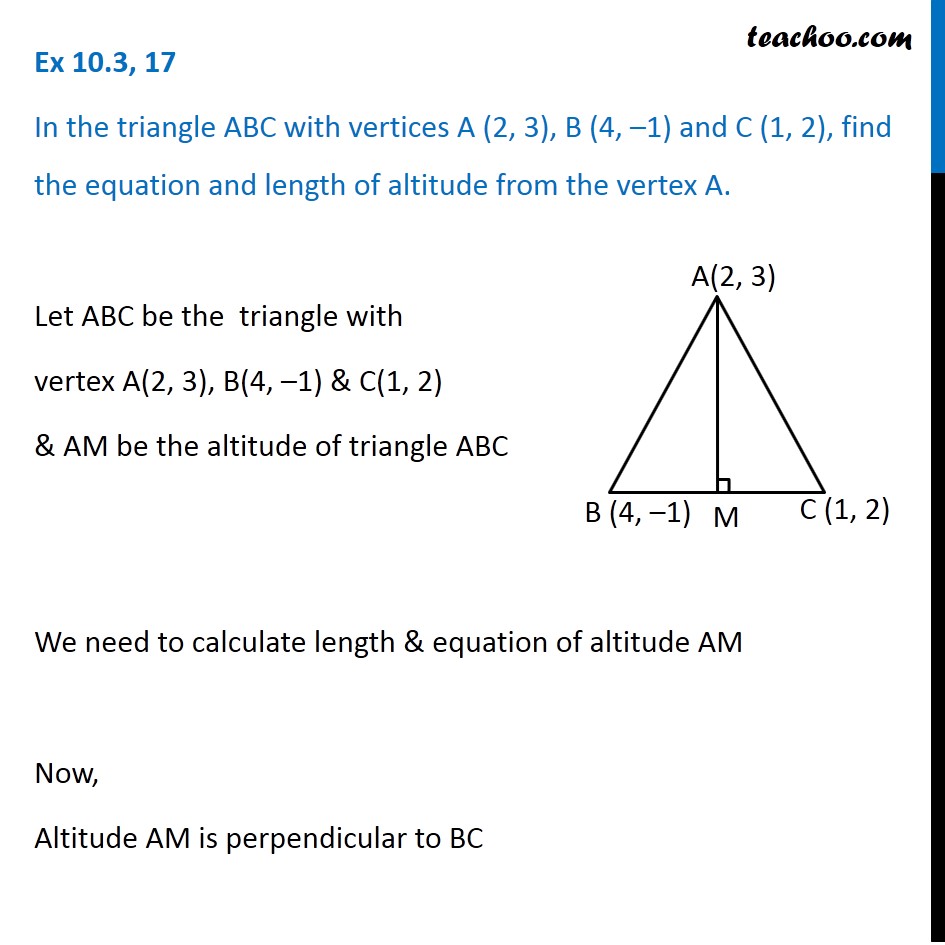



Ex 10 3 17 In Abc Vertices A 2 3 B 4 1 C 1 2




Find The Value Of A 3 B 3 C 3 3abc If 1 A B C 8 Ab Ca 19




Find The Value Of A3 C3 3abc If A B C 15 And Ab Ca 74 Brainly In




Pdf 100 Inequalities Problems Amir Parvardi Academia Edu
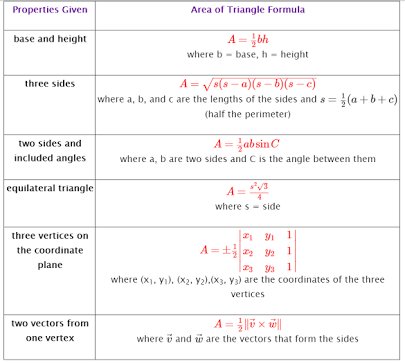



How Do You Solve The Triangle Abc Given A 7 B 3 C 9 Socratic




If Math A B C 0 A 3 B 3 C 3 3 Math And Math A 5 B 5 C 5 10 Math Then Math A 4 B 4 C 4 Math Is Quora




Prove That 1 1 1 A B C A 3 B 3 C 3 A B




Example 3 Let A 1 2 3 B 3 4 And C 4 5 6




Multinomial Expansion




If A B C 3 B2 C2 5 And A3 C3 9 Find The Vakue Of Abc Brainly In




If The Points A 3 A 1 A 2 3 A 1 B 3 B 1 B 2 3 B 1 And C 3 C 1 C 2 3 C 1 Are Collinear For Three Distinct Values A B C And A B C Are Not Equal To 1 Then Find The Value Of Abc Ab Ca 3 A B C




If A B C 0 Then A3 C3 3abc Now What If A B C Is Not Equal To 0 Then How Do Maths Polynomials Meritnation Com




Prove That 1 1 1 A 2 B 2 C 2 A 3 B 3 C 3 A B B C C A Ab Ca



How To Show That 6 Divides A B C Only If 6 Divide A 3 B 3 C 3 Quora




Younesmath12maroc S Blog About Condition A B C Abc 4 Own



Prove That 1 A3 1 1 C3 1 A 1 B 1 C 3 3 Abc Factorisation Maths Class 9




Inequalities From The Word 1995 05




B C A B A C A B C B 3abc A3 C3 A B C A C Prove Maths Determinants Meritnation Com




Proof Of Formula Of Whole Cube Of A B C A B C 3 Youtube




If A B C 0 Then A 3 B 3 C 3 0 How Quora




Inequalities Marathon




Factorisation Of A 2 B 3 C 3 B 2 C 3 A 3 C 2 A 3 B 3 Math Help Boards




If A B C 12 A 2 B 2 C 2 90 Find The Value Of A 3 B 3 C 3 3 Abc Cbse Class 10 Maths Learn Cbse Forum




Using Properties Of Determinants Prove That 3a A B A C B A 3b B C C A C B 3c 3 A B C Ab Ca Mathematics Shaalaa Com




In A Triangle Abc A 3 B 3 C 3 C 2 A B C All Symbol




Prove That A B 3 B C 3 C A 3 3 A B B C C A 2 A 3b 3c 3 3abc Brainly In




Prove A3 C3 3abc A B C B2 C2 Ab Ac Youtube




Prove That 8 A 3 B 3 C 3 2 9 A 2 B 2 Ca C 2 Ab



A 1 3 B 1 3 C 1 3 0 What Is A B C 3 Quora



Prove That A B C 3 A3 C3 3 A B B C C A Polynomials Maths Class 9




Prove That A3 C3 3abc A B C B2 C2 Ab Ac By Taking Lhs Brainly In



Q Tbn And9gcsn3hmt8qz Utmzoqeyjo2k4rnk95kuib8fxbhmd Uvs2llqap Usqp Cau



Using Properties Of Determinants Prove That 1 1 1 A B C A 3 B 3 C 3 A B B C C A A B C Sarthaks Econnect Largest Online Education Community


コメント
コメントを投稿